机器学习：单变量线性回归

你是ABC公司的数据分析人员。ABC公司有全国各地的商业数据，记录不同地区人口和该行业的收入。boss希望在一个新的城市开辟市场，要求你针对该地区的人口做收入的预测。

为了简化自己的环境搭建，建议在windows安装anaconda。现在调包侠要准备调包工作，先倒入各种库。

import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt 

公司的商业数据存储在data.txt中，数据实例如下：

 人口　收入
1.234, 45.2
3.234, 89.2 

实际数据不包括第一行解释。下面我们加载数据文件：

path = os.getcwd() + '\data\data.txt'
data = pd.read_csv(path, header=None, names=['Population', 'Profit']) 

然后我们画一下人口和收入的散点图：

data.plot(kind='scatter', x='Population', y='Profit', figsize=(12,8)) 

产生的如下图表：

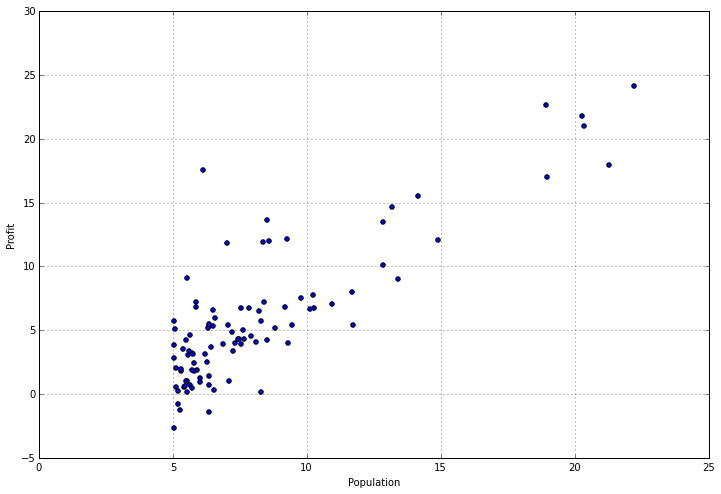
大致看起来，人口越多，收入越大。我们认为两者存在线性关系，进行线性回归。 模型为：y = β0 +  β1 * x，接下来我们就需要求出两个未知参数。
线性回归的损失函数如:

公式对应的代码如下：

 def computeCost(X, beta, y):
    inner = np.power(((X * beta.T) - y), 2)
    return np.sum(inner) / (2 * len(X)) 

上面的beta是向量[β0，β1]，beta.T是beta的转置，X、y都是矩阵。
使用梯度下降法和结合损失函数，函数如下：

 def gradientDescent(X, y, beta, alpha, iters):
    temp = np.matrix(np.zeros(beta.shape))
    parameters = int(beta.ravel().shape[1])
    cost = np.zeros(iters)
    
    for i in range(iters):
        error = (X * beta.T) - y
        
        for j in range(parameters):
            term = np.multiply(error, X[:,j])
            temp[0,j] = beta[0,j] - ((alpha / len(X)) * np.sum(term))
            
        beta = temp
        cost[i] = computeCost(X, beta, y)
        
    return beta, cost 

上面alpha为梯度下降法的步进，iters为迭代的次数。
好了，麻烦的东西贴完了。接下来我们对数据进行整合一下，调整成numpy可以容易计算的矩阵格式。

# 数据列表变成三列，为了方便后面计算。
# ones 人口　收入
# 1, 1.234, 45.2
# 1, 3.234, 89.2
data.insert(0, 'Ones', 1) 

分离训练数据和目标结果：

cols = data.shape[1]
X = data.iloc[:,0:cols-1]
y = data.iloc[:,cols-1:cols] 

现在X值示例为：

# 1, 1.234
# 1, 3.234 

Y的值示例为：

# 45.2
# 89.2 

将数据转为矩阵，方便后续计算：

X = np.matrix(X.values)
y = np.matrix(y.values) 

好了，训练数据矩阵和目标数据矩阵都有了，我们可以开始最关键的调包了。

alpha = 0.01
iters = 1000
beta = np.matrix(np.array([0,0]))
b, cost = gradientDescent(X, y, beta, alpha, iters) 

得到的b就是我们要求得线性回归的参数。
画个看看模型拟合的效果：

x = np.linspace(data.Population.min(), data.Population.max(), 100)
f = b[0, 0] + (b[0, 1] * x)

fig, ax = plt.subplots(figsize=(12,8))
ax.plot(x, f, 'r', label='Prediction')
ax.scatter(data.Population, data.Profit, label='Traning Data')
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size') 

漂亮的结果如下：

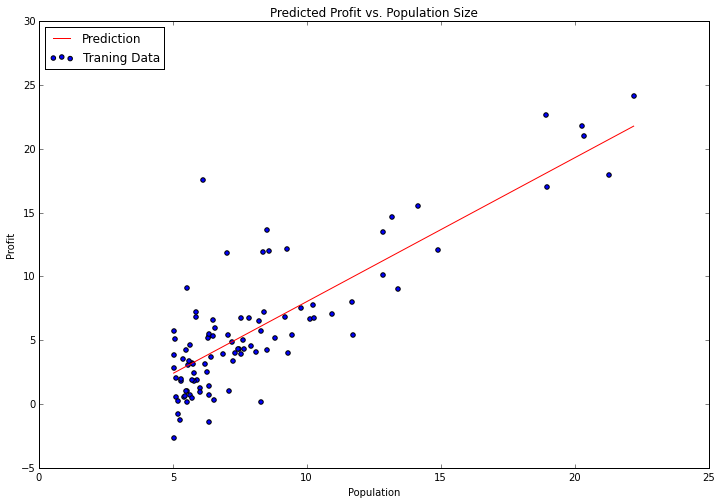
漂亮！调包完成！